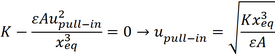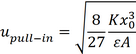<< Click to Display Table of Contents >> Navigation:  Part 2: Electrostatic Transducers I > 2.6 Voltage control and stability

So far we have taken the extensive variables q and x as the independent, controlling variables and we calculated the resulting intensive variables, i.e. the force Fext and voltage u. We did this because the work done at the ports was given by dW=udq in the electrical domain and by dW=Fextdx in the mechanical domain, so that the change in stored energy is given by:

We have seen that by integrating (2.29) using a path integral we can find the energy function U(x, q) of the transducer as a function of x and q. From the energy function we could calculate the intensive variables and the characteristic equations by partial differentiation.

However, in many practical situations it is not the extensive variables that are controlled, or even known, but rather the intensive variables. For example, one could have an external force applied and be curious as to at which position the plates will find their equilibrium position. Or one could have a voltage applied to the capacitor rather than a charge put on the plates. In fact, applying a voltage is much more common than controlling a capacitor by the amount of charge.

In principle, our analysis in the previous section remains valid. So we can still find the energy function as a function of the extensive variables, and then find the intensive variables by taking the derivatives as shown in (2.26) and (2.27). Equations (2.26) and (2.27) relate the four variables q, x, u and Fext to each other, and we can rewrite these equations to express any two variables as a function of the other two. In the case that our capacitor with spring is controlled by a voltage we can rewrite the equations as follows. First, we use (2.27) to find the charge q as a function of the voltage u:

Next, we insert (2.30) into (2.26) to find Fext as a function of the voltage:

We see that the force still consists of a part originating from the capacitor and a part originating from the spring. However, we see that the electrostatic force due to the capacitor is now dependent on x. This makes it much more difficult to find the equilibrium position, that is the position where no external force is needed. We now need to solve the following very non-linear equation:

It turns out that an analytical solution does not exist, so we can only find the equilibrium position xeq for a given voltage u by solving (2.32) numerically. That is, if a solution exists. With increasing voltage the electrostatic force increases. As a result the equilibrium distance decreases which results in a further increase of the force, a further decrease of the distance, a further increase of the force, and so on. With voltage control the parallel plate capacitor can become unstable causing the plates to collapse on top of each other.

We can analyze this by sketching a plot of (2.31) as a function of x and for different voltages u, as shown in Figure 2.6.1. In the figure the initial distance between the plates is x0=1μm. So this is the equilibrium position when no voltage is applied. For a voltage of 0.5V we have the red curve, and we see that there are in fact two values of x where the force is zero. So equation (2.32) has two solutions. One solution is just below the initial position of 1μm. From the slope of the line we can see that this is a stable solution: if we want to increase the plate separation we need to apply a positive force to achieve that. And if we want to decrease the distance we need a negative force, meaning that we really have to push the moveable plate towards the fixed plate. For the other solution, which is around 0.25μm the situation is completely different: if x increases slightly from this point we need a negative force to keep it steady, so without applying a force the plate will move further until it reaches the other equilibrium position. The equilibrium at 0.25μm is marginally stable: the slightest disturbance will cause the plate either to collide on the fixed plate, or to move to the other equilibrium. We see that when the voltage is increased to 0.8V (blue curve) the two equilibrium points approach each other. If the voltage gets too high the curve will no longer cross the horizontal axis and there is no equilibrium position. In that case the moveable plate will collide on the fixed plate. The voltage at which this happens it called the pull-in voltage. The electrostatic force is simply too strong for the spring force to overcome it.

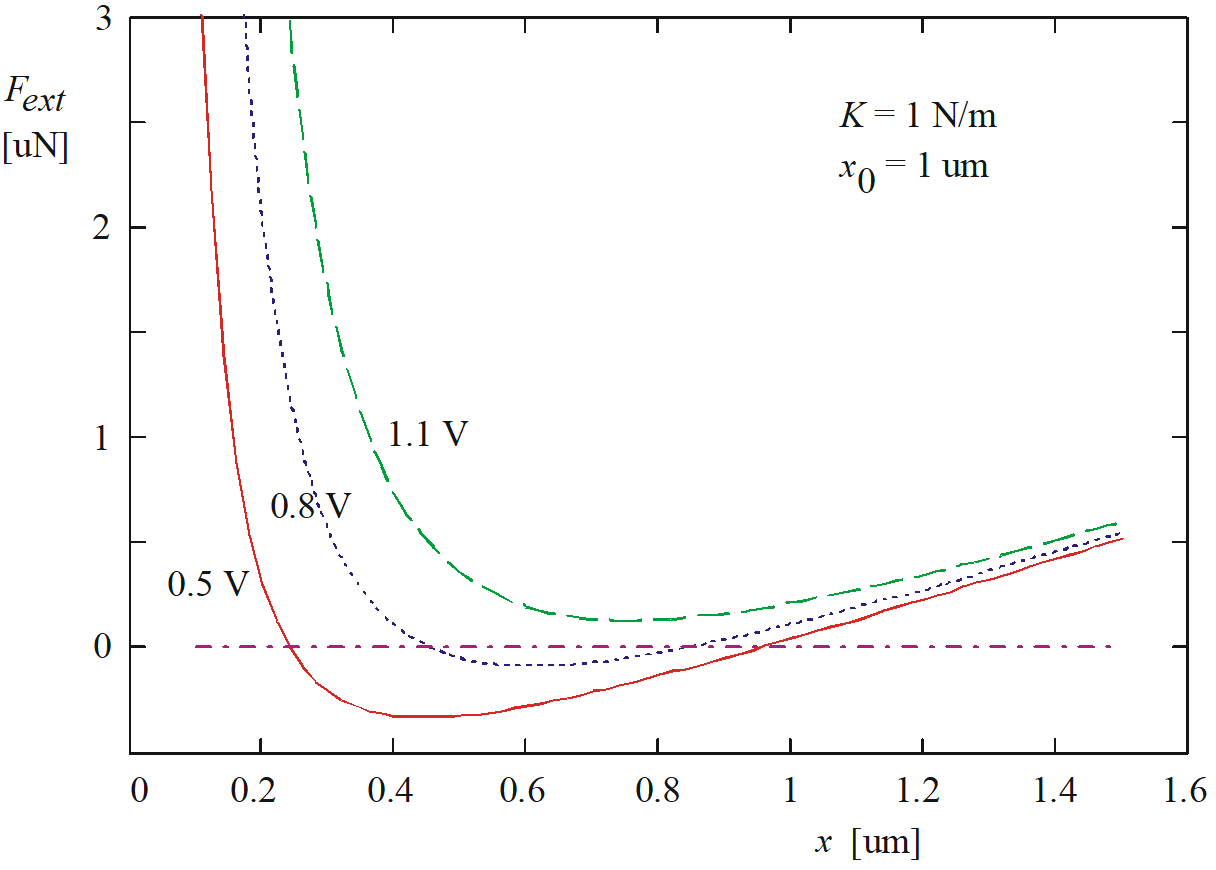
Figure 2.6.1: Plot of the external force as a function of x for three different voltages u. The intersections with the horizontal axis where Fext=0 are the solutions to (2.32). If the voltage exceeds a certain value there are no solutions and the plates will collide on each other.

 

So now we know that when we control the parallel plate capacitor by a voltage the equilibrium position can in principle be found by solving equation (2.32), which we can rewrite into:

The question is whether the obtained equilibrium is a stable equilibrium. We know that at some voltage, the pull-in voltage, the transducer will become instable.

Looking at Figure 2.6.1 we see that at the moment that the transducer becomes instable the curve for Fext will just touch the horizontal axis in one point. If we increase the voltage very slowly, so that the moveable plate approaches the fixed plate in a quasi static way, this pointy will be the position of the capacitor plate just before pull-in. We see that besides the condition that Fext=0 in this point, we also know that the slope of the curve is zero, i.e. the derivative of Fext to x must also be zero. In fact this makes sense: this derivative corresponds to the effective spring constant of the device, indicating how much force you need to apply to displace the moveable plate. If the effective spring constant is zero this means that there is no internal force that counteracts a displacement.

So now we can write, by taking the derivative of (2.31):

At the point where instability occurs this must be zero:

where upull-in is the pull-in voltage. We can now combine (2.35) with (2.33) and this allows us to solve for both the pull-in voltage and the equilibrium position where pull-in occurs:

Try to find this yourself! So we see that when we slowly increase the voltage, pull-in occurs at exactly 2/3 of the original distance between the plates.